115. Two digits
How many n-digit
numbers can be created using only digits 5 and 9, where no three identical
digits stand side by side?
Input.
One number n (n ≤ 30).
Output.
The amount of n-digit numbers.
|
Sample input |
Sample output |
|
3 |
6 |
SOLUTION
dynamic programming
Algorithm
analysis
There are only two desired single-digit numbers: 5 and
9.
There are four desired two-digit numbers: 55, 59, 95 and
99.
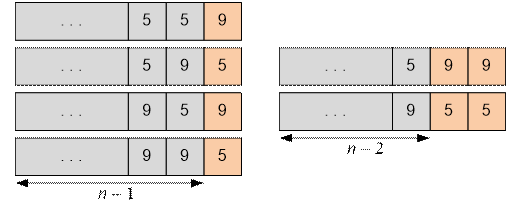
We shall construct the desired n-digit numbers as follows. Take all the constructed (n – 1) - digit numbers and append to
them a digit that does not match their last digit. This way, we obtain n-digit numbers ending in 559, 595, 959 and
995.
To the n-digit
numbers, we will also include those that can be obtained from (n – 2)-digit numbers by
appending two fives or two nines so that three consecutive identical digits are
not obtained. That is, to the n-digit numbers, we add those that end in
599 and 955.
If we denote the number of desired n-digit numbers as f(n), then
we obtain the recurrence:
f(n) = f(n – 1) + f(n – 2), f(1) = 2, f(2) = 4
Example
There are four two-digit numbers: 55, 59, 95 and 99.
There are six three-digit numbers: 559, 595, 959, 995,
599 and 955.
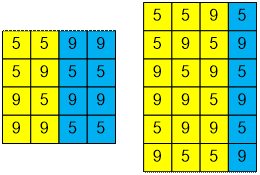
The set of all desired four-digit numbers we can get
from:
·
three-digit
numbers by appending a digit different from the last one: 5595, 5959, 9595,
9959, 5995 and 9559.
·
two-digit
numbers by appending 55 or 99 to them so as not to obtain three identical digits:
5599, 5955, 9599 and 9955.
Algorithm
realization
The
value of f(i) will be stored in cell
m[i].
int m[31];
Read
the input value of n.
scanf("%d", &n);
Store
the values f(1) = 2 and f(2) = 4 in the
array.
m[1] = 2; m[2] = 4;
Compute
the values m[i] (3 ≤ i ≤ n) according to the
recurrence formula.
for(i = 3; i <= n; i++)
m[i] = m[i-1] + m[i-2];
Print
the answer – the value of m[n].
printf("%d\n",m[n]);
Java realization
import java.util.*;
public class Main
{
public static int MAX = 32;
static int m[] = new int[MAX];
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
m[1] = 2; m[2] = 4;
for(int i = 3; i <= n; i++) m[i] = m[i-1] + m[i-2];
System.out.println(m[n]);
}
}
Python realization
Read
the input value of n.
n = int(input())
Initialize a
list m.
m = [0] * 31
Store
the values f(1) = 2 and f(2) = 4 in the
list.
m[1] = 2
m[2] = 4
Compute
the values m[i] (3 ≤ i ≤ n) according to the
recurrence formula.
for i in range(3, n + 1):
m[i] = m[i - 1] + m[i - 2]
Print
the answer – the value of m[n].
print(m[n])